What's it about?
We have performed a round-robin study of surface irregularity measurements of a free-form toroidal window. The measurement tools were a Leitz scanning CMM at Optimax Systems, Inc., an UltraSurf, a non-contact measuring system at OptiPro Systems, a Zeiss scanning CMM at OptiPro Systems, a F25 micro-CMM at Carl Zeiss Industrial Metrology, and an ASI(Q)TM at QED Technologies. Each instrument resulted in a 2.5D surface error map. The measurements were compared with multiple analysis settings. The different analysis settings removed some low frequency height errors, which varied amongst the measurements. This highlights the need for more study to determine the reasons for the differences in the low frequency errors. With the low frequency errors removed, the measurements compared very well, to within 0.2 µm rms.
1. INTRODUCTION
Free-form surfaces are quickly becoming a desired and necessary shape for many refractive and reflective optical systems. Some examples of free-form shapes are toroids, ogives, and other conformal windows. A free-form typically means a shape that is not defined by a standard spherical or aspheric (conic) equation. A free-form shape typically has no rotational symmetry. Departures from a best-fit sphere of a free-form surface vary, but many desired free-form shapes have departures in the range of 1 mm to 10 mm. New and adapted processes have been developed to manufacture these free-form shapes, but without adequate metrology the ability to produce quality surfaces is severely limited.
The purpose of this study is to determine the state of current measurement methods of free-form surfaces. To meet this purpose we have performed a round-robin study measuring the surface irregularities of a free-form shape. In this paper, we review why new measurement methods are necessary for free-form shapes, introduce the methods used to measure the part, review the measurement results, and discuss the variation in the results. In addition, we will discuss general concerns with measuring and specifying free-forms surfaces.
The form of the round-robin study is as follows. First, a design was chosen and Optimax manufactured a toroidal window using grinding and polishing. The surface was polished until free of significant sub-surface damage (gray-free) but the surface was not corrected for surface form error. No specific surface tolerance was used. After manufacturing, the part was measured at Optimax and then the part was mailed to other companies for measurement at their sites. No information was given about the part to each participant other than the nominal shape.
1.1 The shape we chose to measure
We decided to manufacture and measure a toroidal window for this round-robin study. A toroid, which has different radii in orthogonal directions, is a good shape for this study because of its highly free-form nature while still being a shape that is easily defined in equation form (as opposed to a cloud of points). Figure 1 shows a sketch of the toroid to be manufactured and measured. As manufactured the toroid is oversize, at 110 mm by 110 mm square and has a manufacturing defect in thickness. The nominal thickness is 6 mm instead of the designed 5 mm. We believe that this defect will not dramatically affect the round-robin results as most measurements focused on the surface measurements. But for the methods that did measurement thickness, this defect caused a slight headache but was resolved when the correct nominal thickness was used. Figure 2 shows a picture of the toroid. The window is made of fused silica.
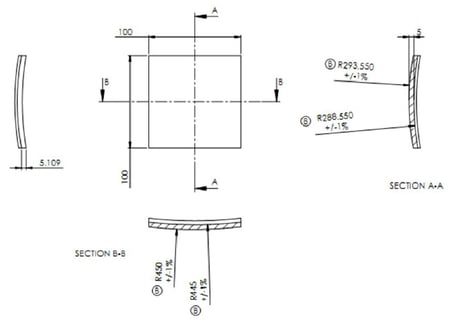
Figure 1 A sketch of the toroid to be manufactured and measured, all units in mm.

Figure 2 A picture of the toroid.
1.2 Desired measurement
The desired measurement is the deviation of the surface from the nominal shape, in a direction normal to the nominal shape as shown in Figure 3 (in profile only). This deviation normal is similar to a typical interferometric measurement of an optical surface. Shown is the profile only, but the full surface map is required for achieving an accurate representation of the surface. A full surface map has a deviation for each point of an equally spaced grid of x,y points across the surface of the optic. The lateral (x,y) spacing, the mm per pixel, is dependent on the measurement method; no minimum spacing was specified for this round robin test, which in hindsight was a planning error. The needed lateral spacing depends on the manufacturing method and the part’s final application.
With this full surface measurement surface corrections and final specification checks are possible. Surface corrections are a standard and critical procedure in optical manufacturing. The part is measured and then specific areas of the part are polished using a sub-aperture polishing method. This procedure is critical to achieving surfaces with low form error, especially for free-form shapes. This is a key reason why accurate surface measurements are needed.
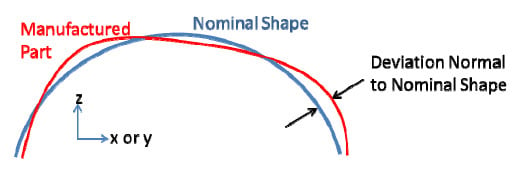
Figure 3 Sketch of the desired measurement: deviation of the manufactured part, normal to the nominal shape.
1.3 Why conventional metrology fails
A commercial Fizeau interferometer is the tool of choice for measuring the irregularity of optical surfaces shown schematically in Figure 4. The transmission sphere produces a transmitted converging test wavefront and a reflected reference wavefront. The test wavefront reflects from the test part and then interferes with the reference wavefront at the detector to form a fringe pattern. This fringe pattern phase shifts through a physical movement of the transmission sphere. The shifted images are collected and the phase of test part is found through simple calculations. The phase is converted to a height deviation with the wavelength of light and information about the optical setup. The surface height map (shown in Figure 4) shows the measured deviation at each camera pixel (which is mapped to a lateral area on the part). The deviation shown is the difference between the test part and a best fit sphere, normal to the nominal shape.
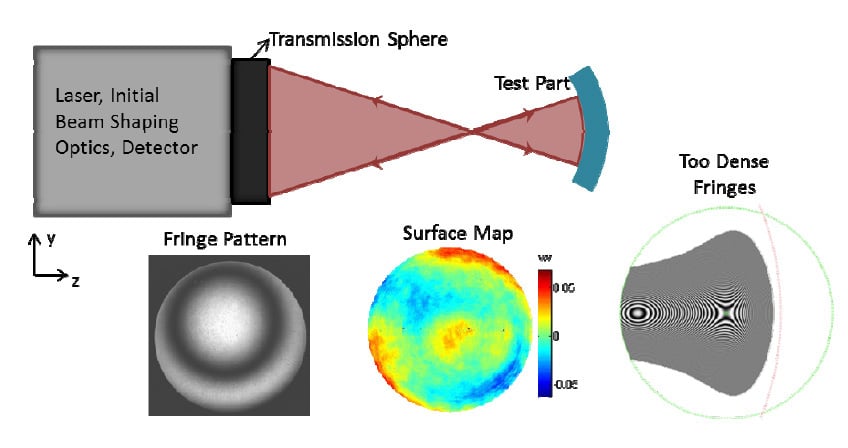
Figure 4 Schematic of a Fizeau interferometer including the resultant fringe pattern and surface height map. Also shown is an example of too dense fringes from QED Technologies.
The number of fringes in the fringe pattern indicates the difference between the test and reference wavefronts. When the differences become large over the same lateral area, the fringes will become very dense. If the fringes reach the Nyquist limit on the camera, the pattern is no longer resolvable. An example of this is shown in Figure 4. The fringes in the center of the part are resolvable, but quickly become non-resolvable. This is the main reason that the typical optical measurement method, interferometry, fails for measuring free-form optical surfaces. The free-form’s high deviation from the spherical reference wavefront results in fringes that are too dense to be resolved.
2. MEASUREMENT METHODS
2.1 Coordinate measuring machine at Optimax
Optimax measured the toroid on a Leitz PMM 866 coordinate measuring machine with certified volumetric accuracy of 1.2 µm + L/400 µm (where L is in mm). The probe is ruby sphere attached to a scanning head which scans at constant force near 0.3 N. The part was held in a vice with minimal clamping force. Each surface of the toroid was measured independently. Each surface was measured with a series of lines. Along the lines (the direction of the scan), the point lateral spacing was approximately 0.5 mm leading to near 17,000 measurement points. The lateral spacing between the lines is approximately 1 mm.

Figure 5 Photograph of the Leitz CMM at Optimax.
For the measurement, the CMM software uses the surface nominal shape (as a solid model) and user input to approximately locate the shape in space. The surface is then scanned with the probe normal to the nominal shape. The CMM software then performs a best fit operation to fit the nominal shape to the measured shape. This is done to remove misalignments between the nominal shape and the measured shape. The report from the CMM is a set of XYZ points for both the nominal and measured shapes and the IJK vectors normal to the nominal shape. The deviation along the normal vector is then calculated in Matlab, outside the CMM software. To calculate this normal deviation, we first find the deviation vector between the measured and nominal points and then project that vector onto the normal vectors using the angle between the deviation vector and the normal vector. This results in an unequally laterally spaced set of normal deviation points. We then fit this set of points to an evenly spaced grid (typically 0.5 mm lateral spacing). This fitting is required for display purposes and for input into typical optical manufacturing equipment. Errors in this fit, from interpolation and from uneven distribution along the slope of the test part are expected to be small compared to the
surface form error.
2.2 Ultra-Surf at OptiPro
OptiPro Systems has been developing the UltraSurf, a non-contact measuring system using state of the art, air-bearing, precision motion control. The five-axis, non-contact single point measurement is flexible enough to handle common metrology problems such as surface roughness, slope error, and high departure from base radius. UltraSurf measures with sub-micrometer non-contact point sensors to collect surface information. Various sensors are commercially available from multiple companies, each with their own distinct optical measuring technology. An optical sensor using low-coherence interferometry with a near infrared laser was used to measure the inside, outside, and thickness of the toroid at a single point. The probe scanned over the toroid point to point, staying normal to the surface at all times. Taking multiple points on the toroid produced a full 2.5D point cloud for both surfaces along with the material thickness. UltraSurf measures in reflection, so surfaces must be parallel to near 2 degrees total in order to measure thickness. The toroid was measured while sitting on a flat plate, convex side up, secured in place by thin double sided tape. All the data was collected in a single measurement.

Figure 6 UltraSurf measuring a large radius concave surface, X,Y,C axes move the part under test, B,Z axes move the noncontact probe.
The measured point clouds were best fit to the toroid shape in software. OptiPro used the equation of the toroid to fit lateral translations, rotations, and radius. Optimizing the radius removes lower order errors from the final data set, and provides the best fit radius that can be used for manufacturing tolerances. In the case of a true freeform, a material offset along the surface normal can be substituted. Both methods are way to separate the shape of the data from the form error. Form error is calculated normal to the surface geometry, which provides a slope insensitive measure of deviation.
After form is removed, the datasets are interpolated to a grid using cubic splines. Interpolation accuracy with this technique is on the order of 1000 times less than the input data. So if the input data is in microns, nanometer scale interpolation artifacts would be expected. Therefore the micron level form error is interpolated instead of the millimeter level raw data. This ensures that interpolation error is insignificant.
2.3 Coordinate measuring machine at OptiPro
OptiPro measured both sides of the toroid with a Zeiss Micura CMM (Figure 7A). The Micura CMM uses a constant force scanning head with less than 200 millinewtons of force to drag a ruby stylus over the surface of the optic. The CMM was qualified to 0.6 micrometers of total accuracy by a Zeiss technician before measurements of the toroid began. The convex and concave sides of the toroid were measured separately. The concave side was measured by placing the toroid on heavy steel v-block, and secured with red wax as shown in Figure 7B. The convex side was measured by directly placing the toroid on the granite base of the CMM and held in place with red wax as shown in Figure 7C. The scanning technique is faster than point to point touch-trigger measurement, although the scan speed should be adjusted to the slope to ensure optimal results. The data was processed and treated in a similar manner to the OptiPro UltraSurf.
Figure 7 (A) Zeiss Micura CMM, (B) Micura scanning the concave side of toroid, (C) Micura scanning convex side of toroid
2.4 F25 coordinate measuring machine at Zeiss
The F25, Figure 8, is a micro-CMM capable of measuring with volumetric accuracy at or better than 0.25 µm + L/666 µm (where L is in mm) and resolution of 1 nm. The probe is a touch stylus with a micro-sphere with probing force down to 0.5 mN/µm. Both surfaces of the toroid were measured with the circular pattern shown in Figure 9. The toroid was set on the three point mount for measurements with the expectation that the low force probe would have no significant effect on the part position. The part was measured in a circular scanning pattern at 0.5 mm per second as shown in Figure 9 with measured point spacing along the circles at 0.5 mm. The data was analyzed in the Zeiss Calypso Software where a best fit analysis was performed to fit the measured data to the nominal shape. Then the deviation between the measured and nominal, normal to the nominal shape, is calculated and reported by the Calypso software. For comparison to the other measurements, this data was fit in Matlab to an equally spaced x,y grid. There are some concerns about the validly of the interpolation in corner sections where data was not takenas shown on the Figure 9b..
Figure 8 The F25 at Zeiss.

Figure 9 (a) Photograph of the toroid during the Zeiss F25 measurement and (b) the measurement locations of the F25 on the part.
2.5 Aspheric stitching interferometer at QED Technologies
QED Technologies measured the convex surface of the toroid on the Aspheric Stitching Interferometer equipped with the new QIS™ interferometer (ASI(Q)™)1. The ASI(Q)™ combines a Fizeau interferometer, an accurate part positioning system, and mathematical stitching algorithms to measure non-spherical and large aperture surfaces. The commercial version of the ASI is used to measure aspheric surfaces, and can measure rotationally-symmetric surfaces with up to 1000 waves (633 microns) departure from best-fit sphere. For this project, QED extended and generalized portions of the stitch process and developed beta software to allow for a proof-of-concept measurement of the toroid. The departure from best-fit sphere of the toroid is nearly 2.5 times larger than the measurable limit of the current ASI(Q). The intent of QED’s measurement of the toroid was to show basic capability and potential, but more development will be needed to fully generalize the measurement process for rotationally-symmetric aspheres to freeform surfaces and improve the accuracy of the low-order figure error.

Figure 10 QED Technologies ASI(Q)™
When the toroid is viewed by the stitching interferometer, only a very small portion of the toroid has resolvable fringes. An example of non-resolvable fringes is shown in Figure 4. By moving the part relative to the interferometer, different subaperture regions on the part become resolvable. This is a key concept of stitching aspheric or free-form surfaces – in a stitching interferometer, the part is moved relative to the interferometer, and a height measurement of overlapping subaperture subapertures with resolvable fringes is captured. Measuring subapertures (as opposed to the complete fullaperture surface) has the following advantages: it reduces the amount of departure from best-fit sphere in a single measurement, it increases resolution by applying all detector pixels over just the subaperture, and it allows local nulling of fringes through ip/tilt/power adjustments – all reducing the fringe density to be measured and enabling measurements of high-departure surfaces over the full aperture. Using the approximate position, the overlapping areas, and complex algorithms, a final full aperture height map of the surface is calculated. The algorithms take into account removal of reference surface errors, optical retrace errors, and positioning errors of the motion axes. Minimal data processing is required after the stitching process is completed. The measured deviation data is captured and reported normal to the surface.
The overlapping measurement areas, called a lattice, for the toroid is shown in Figure 11
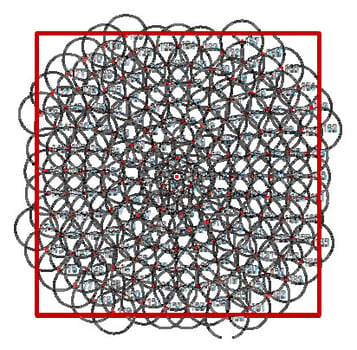
Figure 11 Example lattice, showing the overlapping measurement areas. The red rectangle represents the full aperture of the toroid, while the smaller grey circles represent each subaperture measurement
The concave surface of the toroid was not measured due to time constraints. The full aperture was not measured (the corners are rounded) due to travel limitations on axes that typically are not needed when measuring rotationallysymmetric surfaces. A machine platform specifically designed for measurement freeform surfaces would have appropriate travel limits.
Because high magnification is necessary to resolve the fringes on the toroid, the surface is measured at very high resolution. Six hundred pixels are used for each subaperture measurement, and the final stitch resolution could be as high as 4000 pixels x 4000 pixels. The actual stitched resolution used for the toroid was 1200 pixels x 1200 pixels – more than enough to highlight the high-frequency features on the surface.
3. COMPARING THE RESULTS
3.1 Measurement results
After measurements, each company sent their measurement data to the other companies for analysis. The data presented here was analyzed by Optimax. We will compare the deviation (along the normal) height maps. This height map is a gird of height points plotted on an equally spaced lateral grid. For some measurements, this grid was found through interpolation. It is expected that any errors in interpolation are small compared to the height errors of the surface. But, we may need to re-examine this assumption in the future. For the comparison, some simple data manipulation was required such as rotating the data to match alignments, inverting to match conventions, and masking to remove some outliers.
Figure 12 shows the height maps with piston (the mean value) and tilt (both directions) removed. As shown, there is a large variation in the measured heights, especially in the concave surface. To perform a better comparison, we removed power in the x and y directions as shown in Figure 13. Power in the x and y directions (equivalent to power and astigmatism) indicate a radius error in the toroid and/or a measurement misalignment in some measuring methods. As shown, the measurements look very comparable in most cases. While the ASI(Q) excels at measuring the mid to high frequency features of the toroid, more development is needed by QED to improve the accuracy of the low-order figure error, as evidenced by the data with low-order error included (Figure 12 and Figure 13). It is also possible that the difference in low-order error results from mount-induced distortion or differences in the removal of the nominal shape. To look beyond this difference, we removed the general form of that error (Zernike spherical and Zernike 16) on all the datasets as shown in Figure 14. As shown, the comparison improves and may of the measurements look very similar. Removing spherical and Zernike 16 had little effect on the measured data except with QED ASI data.
Note that some of the measurements show cross areas missing from the measurements. These were put on the part for alignment purposes. Some companies measured the part before the crosses were etched on and some measurement methods were not affected by the crosses. In any case, they can be disregarded.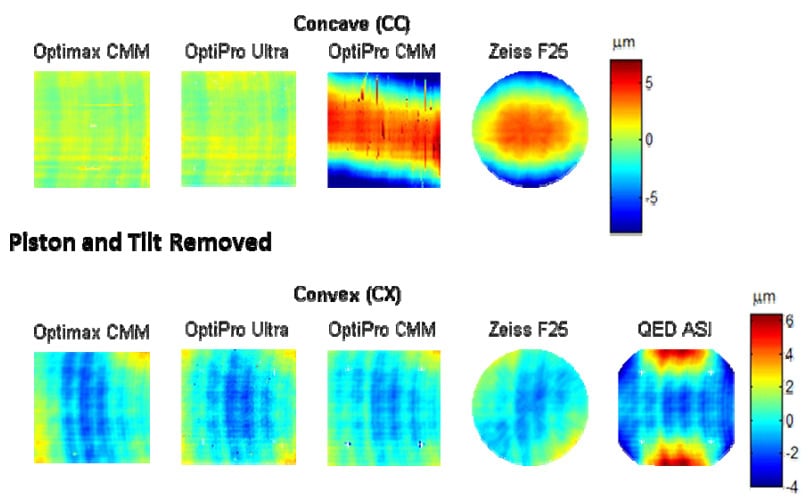
Figure 12 Surface height maps with only piston (mean value) and tilt (both directions) removed for all available measurements. Size is 90 mm by 90 mm.
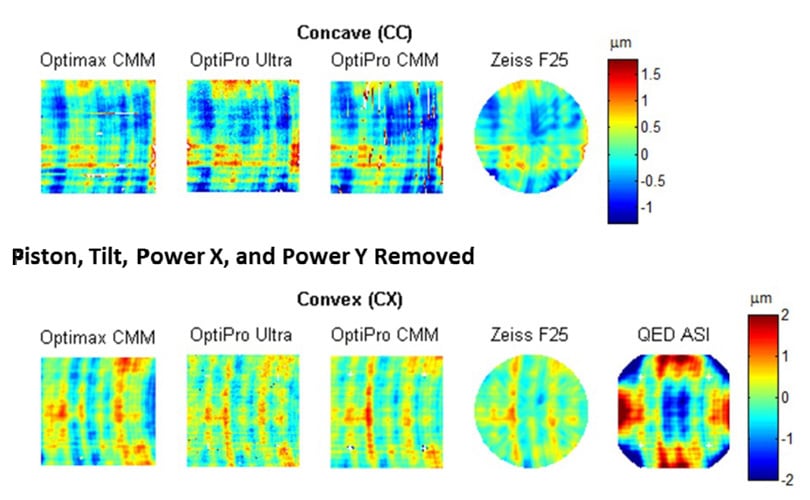
Figure 13 Surface height maps with piston, tilt (both directions), power x and power y (equivalent to piston tilt, power, and astigmatism) removed for all available measurements. Size is 90 mm by 90 mm.
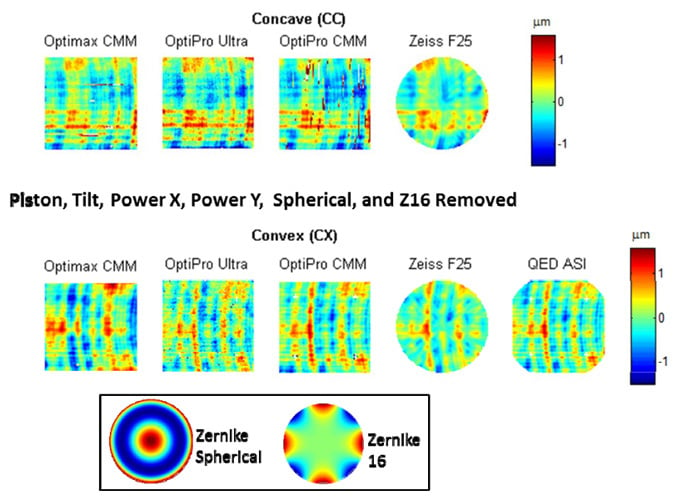
Figure 14 Surface height maps with piston, tilt (both directions), power x, power y, Zernike spherical, and Zernike term number 16 removed for all available measurements. Size is 90 mm by 90 mm.
Figure 15 shows the rms (root-mean-square, Sq) of the height maps for each of the removal conditions. Peak-to-valley was not used due to the large presence of outliers. As shown, the rms values vary considerably expect for the last removal conditions where the peak-to-peak variation was within 0.2 µm rms. Figure 16 shows a standard deviation map (0.5 mm per pixel) of the five convex measurements in Figure 14. The rms of this standard deviation map is 0.21 µm. As shown, there is one obvious vertical feature. The 0.21 µm may be approaching the known accuracy of some of the measurement methods presented here.
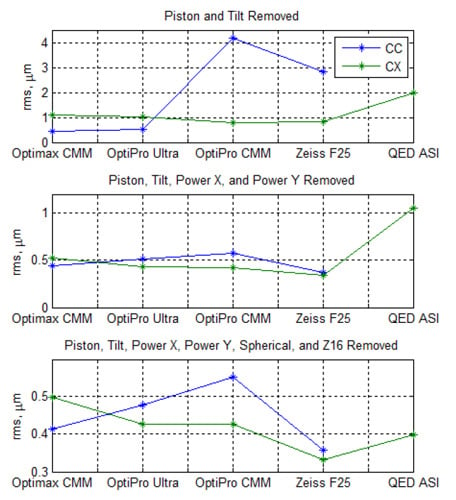
Figure 15 Comparing the rms (root-mean-square) values of the surface height maps.
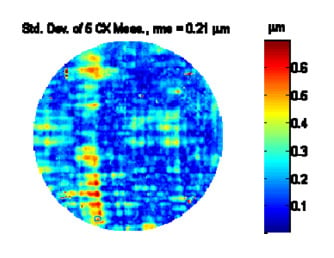
Figure 16 A standard deviation map of the five convex measurements from Figure 14.
3.2 Pixel spacing
The data and measurements presented here vary in the lateral mm per pixel as shown in Table 1. The CMMs show a range of pixel spacing because there is different spacing in the scanning and step-over directions. Clearly, the QED data has a strong advantage in the pixel spacing indicating that much smaller features can be measured. This is shown in Figure 17, the convex measurement by QED with a high pass filter at 2 mm applied. As shown, this measurement is able to pick out the small features. The other measurement methods showed noise at this filter. In hindsight, the large stepover distance in the Zeiss F25 is too large. If we were able to repeat the measurement, we would recommend a smaller step-over. Overall though, the CMM measurements do not reach the pixel resolution of interferometric methods. Analysis is required to determine the required minimum pixel spacing.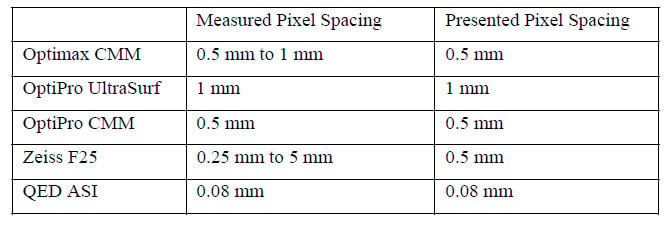
Table 1 The pixel spacing for the measurements and the data.
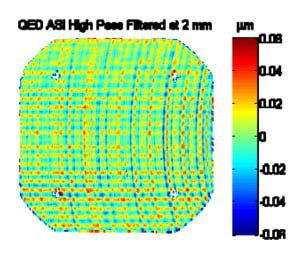
Figure 17 The convex measurement by QED, high pass filtered at a 2 mm cutoff.
3.3 Other measurements
The toroid was examined for other measurements not presented here. These measurements were not presented for space constraints. OptiPro’s UltraSurf has the capability to measure absolute thickness of the part because the probe used measures both surfaces at the same time. They confirmed the thickness measurement with a drop gauge. In addition, the toroid was measured by Zeiss on the METROTOM, a computed tomography instrument. Initial measurements on this instrument indicate that more study is necessary for measuring this type of part on CT system.
4. CONCLUSIONS
The large variation in the measurements in the ‘raw’ data is not easily explained. It is possible that the majority of the differences can be explained by differences in the removing the nominal shape. The coordinate measuring methods should all be capable of correctly identifying the low order form error especially. More study should be done to determine why this variation exists, likely investigating misalignment between the nominal and measured shapes.
For the measurements with the low order form removed, we have found that the measurements vary within 0.21 µm rms. This value is approaching the known accuracy of the coordinate measuring machines. This indicates that the measurements compare well.
Overall though, we see much promise in using tactile tools, such as CMMs in the free-form manufacturing environment with the hope that stitching interferometry will become fully developed for use in free-forms.
5. WHERE DO WE GO FROM HERE?
5.1 Other measurement methods
We are open to having more measurements of the toroid performed. Some possible options include a deflectometry system, the Moore M48 CMM at NIST, the GEMM (Geometry Measuring Machine) at NIST2, and NANOMEFOS3 at TNO in the Netherlands. The main disadvantage of further tests is that they would be not be ‘blind’, that is, the researchers would have some knowledge of the error in the part before they measured. We would not give the measured data to any future testers, but they may see the shape from this paper or presentation.
We invite any party interested in performing a measurement of this toroid window to contact us.
5.2 Manufacturing convergence tests
An indirect method to confirm the accuracy of a measurement is to perform a manufacturing convergence test. The next step in the manufacturing process for this window would be to figure correct the surface form error using a sub-aperture polishing method. The input to sub-aperture polishing is the measurement of the form deviation. We can indirectly confirm the measurement accuracy by seeing if the measured surface error decreases after each sub-aperture polishing step. In this manner, we know the measurement is good because the part keeps getting better.
We have no current plans to perform this test on this specific part as we wish to keep it for a metrology test piece, but some of the companies involved in this work have other plans for manufacturing convergence tests. OptiPro, Optimax, and QED are all working on independent and joint projects in this area. Please contact each of those companies directly for more information on their projects.
5.3 Broader impacts
We would like to use the lessons learned in this study to talk with the community about some of the issues we found. By the community, we mean standards organizations, optical designers, manufacturers, and assemblers.
First, specifications on free-form surfaces need to be considered in more detail than a PV specification. Spherical and planar optical surfaces have separate radius and irregularity tolerances. For a toroid, such a specification would have a separate radius tolerance for each direction and an irregularity tolerance after the power X and power Y are subtracted. What does a radius tolerance look like on a non-toroidal free-form? How can we easily separate a low-order form error from high order form error for other free-forms? Possibly specifications would be Fourier band-pass or Zernike term filtering.
In addition, we believe that the community will need to work on references for free-form surface. For spherical surfaces, it is easy to determine the optical axis. For free-forms, it is not so clear. This is especially relevant in specifications for wedge and low order form error. For example a lateral misalignment between a free-form nominal shape and a perfect surface measurement could show a large form error (the shape is dependent on the surface shape). Whereas a lateral displacement for a spherical optic results in tilt, which is easily identified and removed from the measurement as a misalignment. This must be considered for free-form optical surfaces.
References
[1] Kulawiec, A., Bauer, M., DeVries, G., Fleig, J., Forbes, G., Miladinovic, D., and Murphy, P., “Subaperture stitching interferometry of high-departure aspheres by incorporating configurable null optics,” Optifab 2009, Proc. SPIE TD06-44, May 2009
[2] Machkour-Deshayes, D., Stoup J, Lu, Q.J., Soons, J., Griedmann, U., Polvani, P., “Form-Profiling of Optics Using the Geometry Measuring Machine and the M-48 CMM at NIST,” J. Res. Natl. Inst. Stand. Technol. 111, 373-384 (2006)
[3] Henselmans, R., Cacace, L. A., Kramer, G. F. Y., Rosielle, P. C. J. N., Steinbuch M., “The NANOMEFOS noncontact measurement machine for freeform optics,” Precision Engineering 35(4), 607-624 (2011)
a Optimax Systems Inc., 6367 Dean Parkway Ontario, NY 14519
b OptiPro Systems, 6368 Dean Parkway Ontario, NY 14519
c Carl Zeiss Industrial Metrology, LLC., 6250 Sycamore Lane N, Maple Grove, MN 55369
d QED Technologies, Inc., 1040 University Avenue Rochester, NY 14607
Optifab 2013, edited by Julie L. Bentley, Matthias Pfaff, Proc. of SPIE Vol. 8884, 88840Y © 2013 SPIE · CCC code: 0277-786X/13/$18 · doi: 10.1117/12.2030342
Proc. of SPIE Vol. 8884 88840Y-1
Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 6/14/2018
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use

